Solving The Derivative Of ln(x)
Solving The Derivative Of ln(x)
Derivative Of In: We want to find the by-product of ln(x). The by-productof ln(x) is 1/x, and is actually a well-known derivative that most put to memory. However, it’s always useful to know where this formula comes from, so let’s take a look at the steps to actually find this by-product.
To find the by-product of ln(x), the first thing we do is let y = ln(x). Next, we use the definition of a logarithm to write y = ln(x) in logarithmic form. The definition of logarithms states that y = log b (x) is equivalent to b y = x.
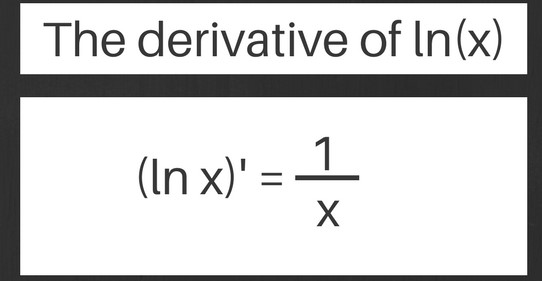
Derivative Of In X
The Natural Log is the logarithm to the base e. where e is an irrational constant approximately equal to 2.718281828. The natural logarithm is usually written ln(x) or loge(x).
The natural log is the inverse function of the exponential function. They are related by the following identities:
eln(x) = x
ln(ex) = x
Derivative Of In(X)

We want to find the by-product of ln(x). The by-product of ln(x) is 1/x, and is actually a well-known derivative that most put to memory. However, it’s always useful to know where this formula comes from, so let’s take a look at the steps to actually find this by-product.
To find the by-product of ln(x), the first thing we do is let y = ln(x). Next, we use the definition of a logarithm to write y = ln(x) in logarithmic form. The definition of logarithms states that y = log b (x) is equivalent to b y = x. Therefore, by the definition of logarithms and the fact that ln(x) is a logarithm with base e, we have that y = ln(x) is equivalent to e y = x.
 |
Okay, just a few more steps, and we’ll have our formula! The next thing we want to do is treat y as a function of x, and take the by-product of each side of the equation with respect to x. We use the chain rule on the left hand side of the equation to find the by-product. The chain rule is a rule we use to take the by-product of a composition of functions, and it has two forms.
 |
The left hand side of the equation is e y, where y is a function of x, so if we let f(x) = e x and g(x) = y, then f(g(x)) = e y. Since the by-product of e to a variable (such as e x) is the same as the original, the derivative of f'(g(x)) is e y. Therefore, by the chain rule, the by-product of e y is e y dy/dx. On the right hand side we have the derivative of x, which is 1.
 |
We have (e y) dy/dx = 1. Now, recall that e y = x. We’re going to use this fact to plug x into our equation for e y.
 |
This gives us the equation (x)dy/dx = 1. We’re getting super close now! Are you as excited as I am? We can divide both sides of this equation by x to get dy/dx = 1/x. The last thing is to recall that y = ln(x) and plug this into our equation for y.
 |
Ta-da! Now, we see that d/dx ln(x) = 1/x, and now we know why this formula for the derivative of ln(x) is true. So what’s our solution? The derivative of ln(x) is 1 / x.
Derivative Of In(2X)
The proof of the derivative of natural logarithm ln(x) is presented using the definition of the derivative. The derivative of a composite function of the form ln(u(x)) is also included and several examples with their solutions are presented.
You have to apply the chain rule that tells us
ddxf[g(x)]=f‘[g(x)]g‘(x).
The f here is the external ln, while the g is the internal ln(x).
The derivative of the logarithm is
ddxln(x)=1x
so the f‘[g(x)]=1ln(x)
and the g‘(x)=1x.
The final result is
ddxln(ln(x))=1ln(x)
1x=1xln(x).
Derivative Of In(X+1)
THE SYSTEM OF NATURAL LOGARITHMS has the number called e as it base; it is the system we use in all theoretical work. (In the next Lesson, we will see that e is approximately 2.718.) The system of natural logarithms is in contrast to the system of common logarithms, which has 10 as its base and is used for most practical work.
We denote the logarithmic function with base e as “ln x.”
ln x = logex.
y = ln x implies e y = x.
In other words, this logarithm function —
y = ln x
— has for its inverse the exponential function,
y = ex.
Here are the inverse relations:
ln ex = x and eln x = x.
And the logarithm of the base itself is always 1:
ln e = 1.
(Topic 20 of Precalculus.)
The function y = ln x is continuous and defined for all positive values of x. It will obey the usual laws of logarithms:
1. ln ab = ln a + ln b.
| 2. ln | a b |
= ln a − ln b. |
3. ln an = n ln a.
(Topic 20 of Precalculus.)
Like all the rules of algebra, they will obey the rule of symmetry.
For example,
n ln a = ln an.
The derivative of ln x
We will now apply the definition of the derivative to prove:
| d dx |
ln x | = | 1 x |
In the course of the proof, we will see that it becomes necessary to define the base of the system of natural logs, the number we call e, as the following limit:
![]()
A limit in the proof will have that same form.
Later, we will call the variable x rather than v. And in the next lesson, upon changing the variable from v to ![]() , the familiar definition follows.
, the familiar definition follows.
Here is the difference quotient:
| according to the 2nd law; | |||
| = | 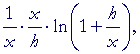 |
on multiplying by x/x; |
| = | 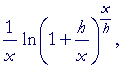 |
according to the 3rd law. |
We now take the limit as h approaches 0.
| = | 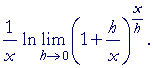 |
| The limit does not apply to | 1 x |
, because h is the variable |
| that is approaching 0. | 1 x |
is a constant factor. |
We now define that limit to be the base of the natural logarithms, the number we will call e. (That limit is the one above, with v = ![]() ; when
; when ![]() 0,
0, ![]()
![]() 0.)
0.)
Which is what we wanted to prove.
What is the derivative of ln 1 x?
To apply the Chain Rule, set u u as 1−x 1 – x . The derivative of ln(u) ln ( u ) with respect to u u is 1u 1 u .
What is the derivative of the natural log?
The derivative of the natural logarithmic function (ln[x]) is simply 1 divided by x. This derivative can be found using both the definition of the derivative and a calculator.
